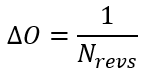10. Order Domain Processing¶
10.1. What is order analysis?¶
- Analysis of mechanical systems with rotating components
- Engines (reciprocating & turbine), transmissions, motors, rotors, turbines, pumps, compressors, bearings, gear boxes, washing machines, dryers, mixers, etc.
- Many noise and vibration signal components are directly related to the rotating speed
- Imbalance, misalignment, gear mesh, bearing defects, loose coupling, resonance, etc.
- Order analysis normalizes the measurements to the rotating speed to better dissect these signal components
10.2. Benefits of Order Analysis as Compared to Time Based FFT Processing¶
- Accurately analyze data that contains time variant frequency components
- Accurate phase relative to a physical location
- Leakage free synchronous analysis
- Insensitive to shaft slew rates
- Separation of synchronous and non-synchronous components
- Analysis of fractional order components
- Removal of random non-synchronous noise via synchronous averaging
- Correlation with other angular domain acquired data, e.g., blade tip timing
10.3. Order Analysis¶
Order Analysis (or order tracking) is a method whereby the signal is sampled according to its frequency variation.
10.4. Test Cases¶
- Evaluation test cases to ascertain algorithm suitability
- Slow sweep rate, single (1 EO) order, SDOF response
- Application: Power gen, machine vibration, rotor balancing
- Desire: Accurate magnitude & phase to the 1/REV
- Fast sweep rate, rich order content, SDOF response
- Application: Aeromechanics, blade vibration
- Integral orders closely spaced representing an asymmetric or non-uniform stator configuration
- Desire: Accurate magnitude, minimize sensitivity to processing options
- Crossing orders
- Application: Machinery vibration & aeromechanics (mode crossing)
- Multi-shaft machine, orders intersecting from 2 or more shaft speeds
- Constant frequency intersecting with constant order response
- Desire: Accurate magnitude track at crossings
- Slow sweep rate, single (1 EO) order, SDOF response
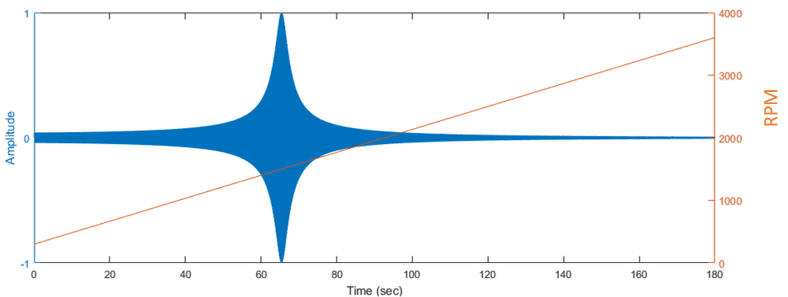
10.4.1. Case 1: Slow Sweep Rate, 1 EO¶
- Acquisition settings
- Fs = 10240
- Δ t = 60 seconds
- Order: 1
- Sweep from 300 to 3,600 RPM over 300 seconds (11 RPM/s)
- Magnitude = 1.0, Q = 25, Φ 0 = 0 °
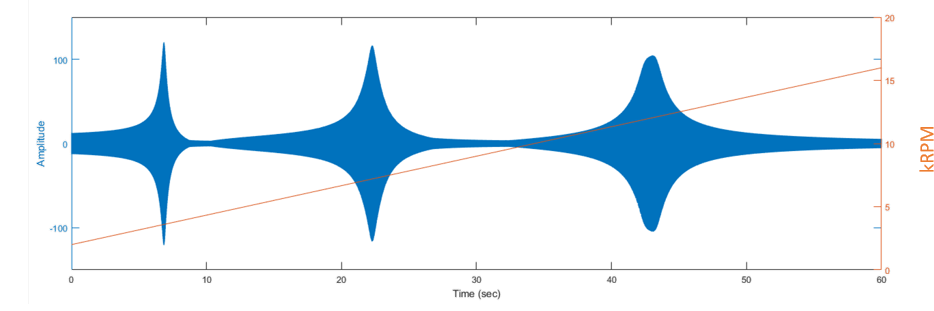
10.4.2. Case 2: Fast Sweep Rate, Multi EO¶
- Acquisition settings
- Fs = 81920
- Δ t = 60 seconds
- Orders: 59, 60, 61 w/ SDOF resonances at 3 different speeds
- Sweep from 2,000 to 16,000 RPM over 60 seconds (233 RPM/s)
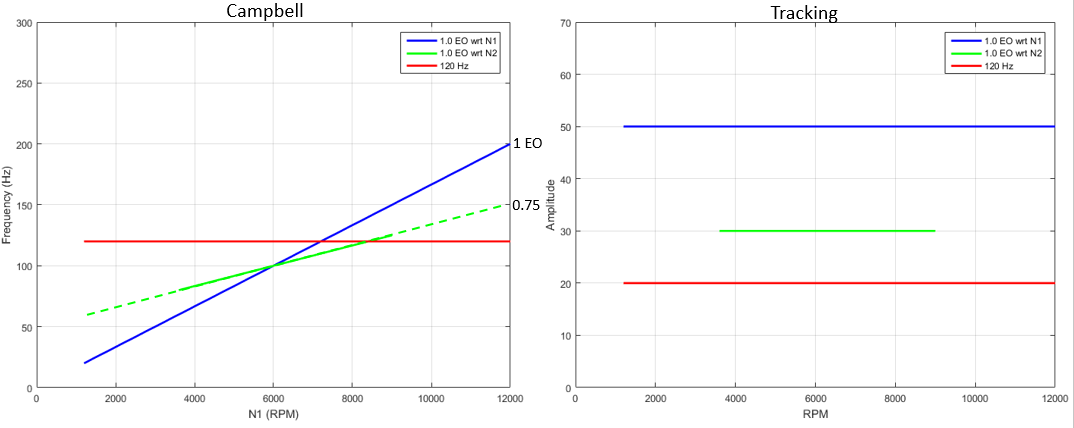
10.4.3. Case 3: Crossing Orders¶
- Many applications contain multiple rotating components
- High/low spool gas turbine engines
- Gear boxes
- Multi-stage centrifugal pumps driven by a bull gear
- Drive trains
- Vibration may be present that is synchronous with one or more shaft frequencies or a combination of shaft frequencies
- Desire to decouple the vibration response(s)
10.5. Processing Techniques¶
10.5.1. Fourier Transform Based Order Tracking (Discrete Order Transform [DOT] in DX)¶
Uses time domain sampled data and the FFT to determine orders
Block size is constant, therefore not related to the rotational speed of the machine
User input of order resolution is purely used as a (frequency) screening criteria, actual minimum order resolution is based on signal processing settings
- Major limitations
Limited order resolution at “low” RPM values, minimum obtainable order resolution based on signal processing:

Note
The factor 3.0 is a scalar on the resolution due to use of any window other than Rectangular. The factor is the result of smearing of energy due to the window. A lower value (2.0) can be used for a Hanning or other windows with a narrow main lobe.
Low enough RPM may result in frequency extraction (based on low orders) < minimum available frequency due to window effects near DC
Requires slow sweep rates to reduce smearing
10.5.2. Computed Order Tracking (COT in DX)¶
Uses synchronously resampled data and the FFT to perform order analysis
- COT processing resamples, via up sampling, the (constant time sampled) signal data at a constant angle
- Requires knowledge of rotor angular position (over the revs)
- Accurate phase requires knowledge of 1/REV phase crossing sample/time
- Provides constant order resolution over the entire speed range
- Order extraction performed on angular resampled data
- Frequency -> Order
- FFT spectrum -> Order spectrum
- Frequency resolution -> Order Resolution
- Frequency bandwidth -> Order bandwidth
- N(samples) -> N(revs)
Similar to a time domain FFT where the ensemble size dictates the frequency resolution, the number of revs dictates the order resolution for order domain analysis, i.e.,